![]()
|
|
This lesson is intended to help you explain what a linear conversion factor does convert any time unit into another time unit explain and show how units cancel in a unit conversion |
All measurements are made using some kind of tool or device. These tools are calibrated with some measurement scale. The units for the scale match the kind of quantity we are measuring. Often length is measured with a simple tape measure or ruler in inches or centimeters. Time is measured with stop watches, clocks, calendars, in units of seconds, minutes, hours weeks, etc. Computations can be verified by checking the fate of units (how they do or do not cancel) in the process. Conversion factors are part of this procedure where one unit is cancelled and a new unit is introduced. This is a property we see when working with fractions. In fractions when the same number appears in the top and bottom of the fraction they can be cancelled out with no change in the value of the fraction. An example of this is the fraction (4 x 7) / 4 = 7 where the '4s' cancel. The unit conversion procedure depends on treating words just like numbers. If identical words appear in both the top and bottom of a fraction they can be cancelled out just like numbers. Conversion factors are fractions too. They have a value of "1". The two parts of the factor are equal in size but have different numbers for the units. Here are some familiar examples of time equalities or conversion factors.
The unit conversion procedure depends on uing these kinds of equalities. Every equality can be written two ways as a fraction. For example 1 day = 24 hours can be used two ways (1 day / 24 hours ) = 1 or (24 hours / 1 day) = 1 The first factor is used to convert hours to days and the second one is used to convert days to hours. EXERCISE How many hours are there in 6 days? ? hours = (6 days) X (24 hours / day ) = 144 hours
|
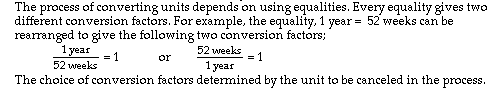
![]()